#和

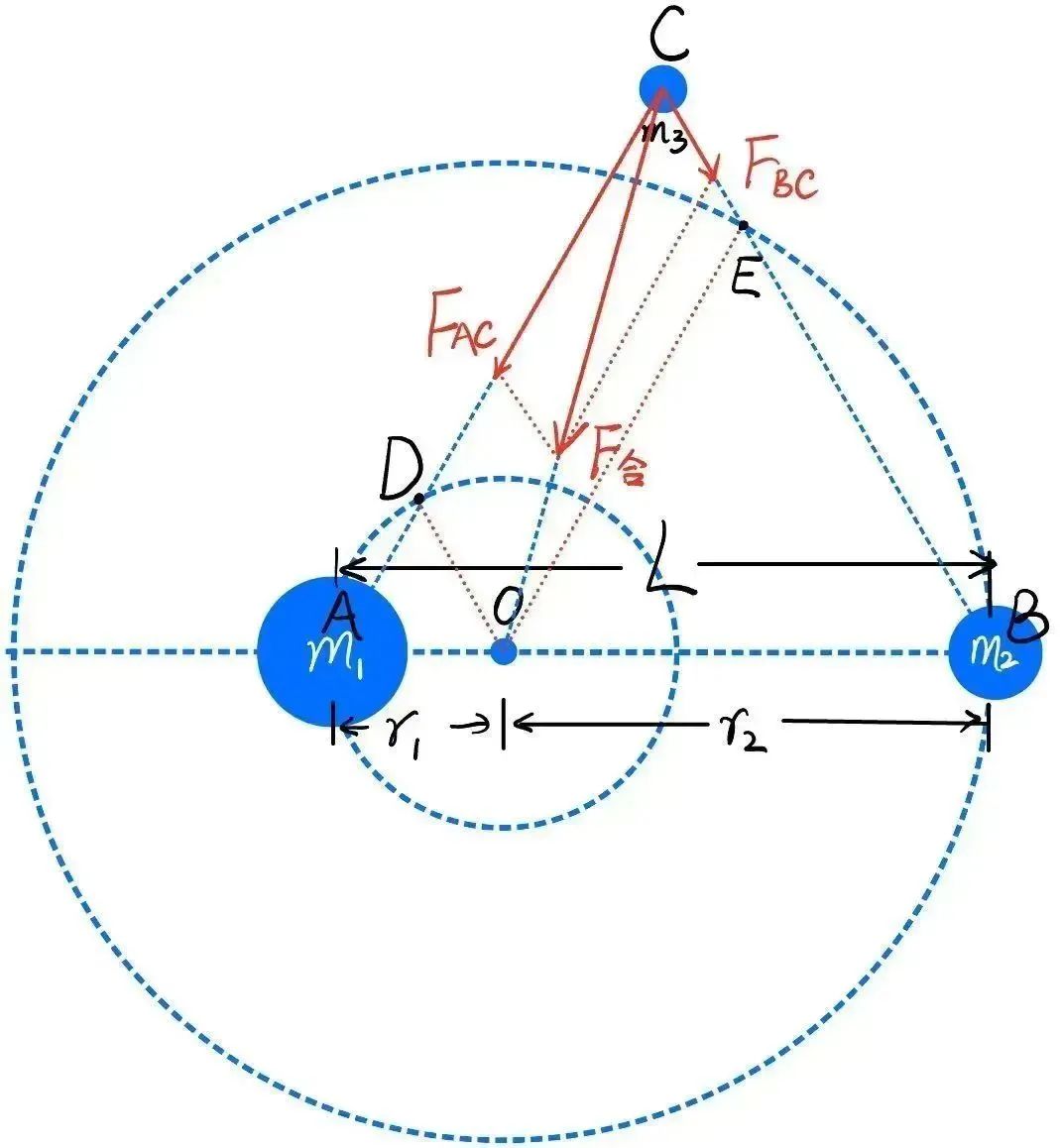
这部分是我觉得拉格朗日最牛的地方。先想象在可以构成等边三角形的地方放置一个，然后我们反过来证明，和在这个地方产生的引力刚好能为提供向心力。

首先是证明合力方向指向公转中心O。由于，又因为，所以力合成的平行四边形和平行四边形CDOE是相似的，这样就证明了合力指向O点。

接着是证明合力大小刚好提供向心力。你当然可以套余弦公式把合力的大小和的长度算出来，来验证它们是符合圆周运动的运动方程。但更优雅的方式是，验证它们所受到的引力加速度总与公转半径成正比。第一个等号已经成立。代入第一个等号你会发现，用矢量的语言不仅说明了大小关系，还再一次验证了合力方向指向O点。

再仔细想想，上述利用矢量关系的推导过程是否绝对依赖于和这个假设呢？你不妨试试把系统的公转中心放在三者的质心上，并重新考虑对另外两个物体的引力，会发现上述关系依然成立，之后总可以求出一个角速度，使得三者一起绕着质心公转。所以对于任意三体系统，这种等边三角形的圆周运动模式都是成立的。

木星的轨道上存在两群小行星，统称为特洛伊群，其中运行在木星“前方”的为“希腊群”，运行在木星“后方”的为“纯特洛伊群”。这两群小行星所处的位置，正是拉格朗日点和。上图中紫色的部分是希尔达小行星群，它们的三角形轨道与木星形成2:3的轨道共振。希尔达小行星的远日点可能是L3、L4、L5 这三个拉格朗日点，当它们连续绕太阳旋转三圈，会相继通过这三个点。